2020年人教版高中必学二数学期末模拟试题
1、选择题(本大题共12小题,共60.0分)
故选:C.
借助倾斜角与斜率的关系即可得出.
本题考查了倾斜角与斜率的关系,是基础题.
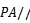 B.
B. 
C.
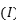 D.
D. 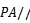
于是可排除,A,B,C.
只有D符合.
故选:D.
令直线
本题考查函数的图象,理解函数的定义是重点,即概念域中任意一个自变量对应唯一的函数值,是基础题
C.
故选:C.
先假设圆的方程
本题的考试知识点是圆的规范方程,主要考查待定系数法求圆的规范方程,是基础题.
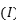 B.
B. 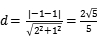
C.
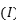 D.
D. 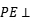
故选:D.
依据零点存在定理,对于B,在零点的左右附近,函数值不改变符号,即可得出结论.
本题考查零点存在定理,考查学生剖析解决问题的能力,是基础题.
对于A,
对于B,
对于C,
对于D,
故选:A.
依据题意,依次剖析选项中函数的概念域与单调性,综合即可得答案.
本题考查函数的单调性的判断,重点是学会容易见到函数的概念域与单调性,是基础题.
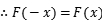 B.
B. 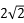 C.
C. 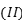 D.
D. 
所以函数的图象是
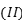 .
.故选:C.
判断函数的奇偶性,借助指数函数的特点判断即可.
本题考查函数的图象的判断,函数的奇偶性与基本函数的特点的考查
由两直线平行得,
故选:B.
依据两直线平行求得k的值,再求两直线之间的距离.
本题考查了直线平行与平行线之间的距离应用问题,是基础题.
C.
故D是不对的,
故选:D.
先求出
本题考查了反函数的概念和对数函数的运算性质,是基础题.

B.
C.
D.
|
【答案】C
【分析】解:由已知可得该几何体为圆柱,
且圆柱的底面直径为2,高![]() ,
,
即圆柱的底面半径![]() ,
,
故该几何体的侧面积![]() .
.
故选:C.
由已知中的三视图可得该几何体是一个底面半径为1,高为4的圆柱,代入圆柱的侧面积公式,可得答案.
本题考查的要点是由三视图求面积,其中依据已知中的三视图剖析出几何体的形状及底面半径,高等几何量是解答的重点.
解得
故选:A.
依据幂函数的图象与性质,列出方程求出满足题意的m值.
本题考查了幂函数的概念与性质的应用问题,是基础题.
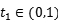
由图可知,
故选:C.
在同一坐标系中分别作出
函数的零点存在性问题常见的方法有三种:一是用定理,二是解方程,三是用图象.
C. 若
在A中,若
在B中,若
在C中,若
在D中,若
故选:D.
在A中,l与
本题考查命题真伪的判断,考查空间中线线、线面、面面间的地方关系等入门知识,考查运算求解能力,考查函数与方程思想,是中档题.
故答案为:
可以求出集合A,然后进行交集的运算即可.
考查描述法的概念,绝对值不等式的解法,与交集的运算.
当
即当
则
故答案为:
依据奇函数的性质借助
本题主要考查函数奇偶性的应用,借助奇函数
故
故答案为:
依据指数函数,对数函数的性质分别判断a,b,c的取值范围进行判断即可.
本题主要考查函数值的大小比较,结合指数和对数函数的性质判断a,b,c的范围是解决本题的重点.
又由圆
圆心
点P是圆
故答案为:2.
依据题意,求出圆
本题考查直线与圆方程的应用,涉及直线与圆的地方关系,依据圆与圆的地方关系求出m是解决本题的重点,是基础题
解得
则
解得
故直线l的方程为
本题考查了直线和垂直和直线的截距,是基础题.
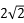 |
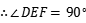 解:(Ⅰ)
解:(Ⅰ)又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD.P⊂平面PAD.
∴PE⊥平面ABCD;
(Ⅱ)取PC的中点H,连接DH,FH,
在三角形PCD中,FH为中位线,可得FH∥BC,
FH=
由DE∥BC,DE=
可得DE=FH,DE∥FH,
四边形EFHD为平行四边形,
可得EF∥DH,
EF⊄平面PCD,DH⊂平面PCD,
即有EF∥平面PCD.
(Ⅲ)∵PA⊥PD.PA=PD=2.∴AD=
∵PE⊥平面ABCD,
∴VP-ABCD=
(Ⅱ)取PC的中点H,连接DH,FH,运用中位线定理和平行四边形的判断和性质,结合线面平行的断定定理,即可得证.
(Ⅲ)可得PE⊥平面ABCD,即VP-ABCD=
本题考查线面和面面的地方关系及体积计算,考查线面平行、垂直的断定和性质,与面面垂直的判断和性质,注意运用转化思想,考查推理能力和空间想象能力,是中档题.
可化为:
即不等式:
本题考查指数函数,考查函数的奇偶性,考查不等式的解法,是中档题
 |
又
又
本题考查了空间中的平行与垂直问题,解题时应明确空间中的线线、线面、面面之间的垂直与平行的互相转化关系,是基础题目.
本题考查二次函数、对数函数、指数函数的性质图象,考查学生灵活运用常识解决问题的能力,属中档题
 解:
解:若圆C被x轴截得的弦长为
则圆C的规范方程为:
过点P作圆C的切线PQ,则
当
此时
本题考查直线与圆方程的综合应用,重点是求出C的方程,是基础题.







