![]() 5.因动点产生的平行四边形问题
5.因动点产生的平行四边形问题
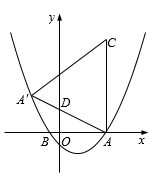
1.如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 轴,交直线
轴,交直线![]()
![]() 于点
于点![]() .
.
(1)求该抛物线的分析式;
(2)求点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 的坐标,断定点
的坐标,断定点![]() 是不是在该抛物线上,并说明理由;
是不是在该抛物线上,并说明理由;
(3)点![]() 是抛物线上一动点,过点
是抛物线上一动点,过点![]() 作
作![]() 轴的平行线,交线段
轴的平行线,交线段![]() 于点
于点![]() ,是不是存在这种点
,是不是存在这种点![]()
![]() ,使四边形
,使四边形![]() 是平行四边形?若存在,求出点
是平行四边形?若存在,求出点![]() 的坐标;若没有,请说明理由.
的坐标;若没有,请说明理由.
分析:(1)∵抛物线![]() 与
与![]()
![]() 轴交于
轴交于![]() 、
、![]() 两点[来源:Z#xx#k.Com]
两点[来源:Z#xx#k.Com]
∴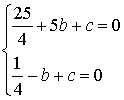 解得
解得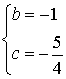
∴抛物线的分析式为![]()
(2)

过点![]() 作
作![]() 轴于
轴于![]() ,
,![]() 与
与![]() 交于点
交于点![]()
∵点![]() 在直线
在直线![]() 上,
上,![]()
∵点![]() 和
和![]() 关于直线
关于直线![]() 对称,
对称,![]() ,
,![]()
![]()
![]()
![]() ,
,
![]()
在![]() 和
和![]() 中
中
![]() ,
,
![]()
![]()
又![]() ,
,![]()
![]() ,即
,即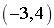
![]()
![]() 点
点![]() 的坐标为
的坐标为![]()
当![]() 时,
时,![]()
∴点![]() 在该抛物线上
在该抛物线上
(3)存在
理由:设直线![]() 的分析式为
的分析式为![]()
则 解得
解得
∴直线![]() 的分析式为
的分析式为![]()
设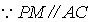 ,则
,则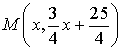
![]()
∴要使四边形![]() 是平行
是平行![]() 四边形,仅需
四边形,仅需![]()
又点![]() 在点
在点![]() 的上方,
的上方,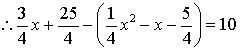
解得![]() (不合题意,舍去)
(不合题意,舍去)
当![]() 时,
时,![]()
∴当点![]() 运动到
运动到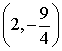 时,四边形
时,四边形![]() 是平行四边形
是平行四边形







